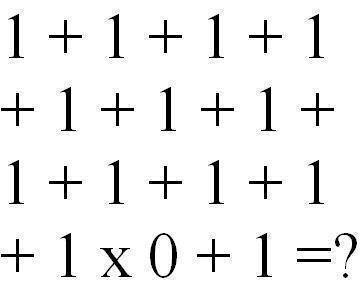Sui social network girano giochini matematici più meno simpatici o divertenti.
Quello che un mio amico ha girato di recente ha fatto il giro delle condivisioni, come tanti.
Quello che veramente colpisce è quante persone lo abbiano sbagliato.
Personalmente, da matematico, posso anche indignarmi per questo, ma in realtà quello che realmente mi indigna è il come chi lo ha sbagliato ha reagito quando qualcuno gli ha fatto notare l’errore.
Il quesito è il risultato di questa espressione
1+1+1+1+ 1+1+1 +1+1+1+1 +1*0 +1 = ?
Alle elementari ci viene insegnato che esiste una priorità tra gli operatori in una espressione. Per cui in caso di ambiguità per prime, alla stessa priorità, vanno eseguite le moltiplicazioni e le divisioni da sinistra verso destra, poi le addizioni e e sottrazioni, sempre da sinistra verso destra.
Se qualcuno di voi mi dicesse che è SOLO una convenzione di forma, gli direi che prende una clamorosa cantonata, tanto quanto la prenderei io se scrivessi “speriamo che non piovi”.
In matematica la forma è sostanza.
Seguendo questa regola il primo passo è eseguire l’unica moltiplicazione presente:
Pertanto
1+1+1+1+ 1+1+1 +1+1+1+1+1*0+1 = 1+1+1+1+ 1+1+1 +1+1+1+0+1
Il secondo passo è effettuare la somma, segue che
1+1+1+1+ 1+1+1 +1+1+1+1+0+1 = 12
Una risposta sbagliata che ho letto al quesito è 1.
Da quale errato calcolo deriva?
Da un errore di priorità e di lettura.
Ossia violando le regole di cui sopra, l’aspirante solutore ha sommato 12 volte 1 e poi ha moltiplicato tutto il risultato per zero e poi ancora sommato 1.
Errato.
In pratica è come se avesse letto
(1+1+1+1+ 1+1+1 +1+1+1+1)*0 +1 = ?
Ossia ha introdotto in modo arbitrario la parentesi tonda nel posto sbagliato, mentre la parentesi sottintesa in realtà era
1+1+1+1+ 1+1+1 +1+1+1+1+(1x0)+1 = ?
Ora qualche furbacchione ha pure detto: ma perché non c’è la parentesi nell’espressione?
La risposta è che la matematica non spreca simboli, come ogni buon linguaggio.
La priorità tra gli operatori è il livello base. Se tale priorità deve cambiare allora si introducono le parentesi per evitare ambiguità.
In questo caso non è necessario perché chi ha scritto l'espressione ha voluto comunicare un calcolo che porta al numero 12, non un altro.
A tal fine scrivere 1+1+1+1+ 1+1+1 +1+1+1+1+(1x0)+1 è nella comunicazione matematica una ridondanza tanto quanto lo è nella lingua italiana scrivere “lo guardò con gli occhi”.
Ora mi chiedo, il cattivo uso di un tempo verbale è esecrabile. Perché non deve essere l’errato uso degli strumenti della matematica?
Perché è più socialmente accettabile?
Non voglio scomodare concetti più avanzati, però tento un ragionamento più formale.
Tra i numeri sappiamo per certe due cose, lo zero è l’unico numero che conosciamo che:
- Qualsia numero, indicato con il simbolo a, sommiamo a zero, il risultato dell’operazione è il numero stesso. In sintesi a + 0 = a, per qualsiasi numero a
- Qualsiasi numero, indicato con il simbolo a, moltiplichiamo per 0 il risultato dell’operazione è 0. In sintesi a * 0 = 0, per qualsiasi numero a.
Sapendo questo dimostriamo la falsità del risultato
1+1+1+1+ 1+1+1 +1+1+1+1+1x0+1 = 1.
Se per assurdo fosse vero
Allora
a = 1+1+1+1+ 1+1+1 +1+1+1+1 = 11
b= 1
Ossia avremmo che
a + b*0+1 = 1
11+1*0 +1 = 1
Possiamo semplificare sottraendo 1 a entrambi i membri
Allora avremmo
11 + 1*0 = 0
Quindi, portando a destra 11
1 * 0= -11
L’assurdo è che avremmo trovato un numero (1) che moltiplicato per zero dà un altro numero (-11). Oppure, assurdo ancora più grande, che 0 = - 11 e contemporaneamente 0 = 11 (moltiplicando ambo i membri per -1).
Si potrebbe estendere il ragionamento in termini simbolici dicendo che avremmo trovato una coppia di numeri a e b per cui
a+ b*0 = 0
ossia b*0 = -a con a e b diversi da zero,
ossia 0 =-b/a cioè avremmo ottenuto zero da due numeri diversi da zero!
Quindi non solo cadrebbe l’unicità dello zero, ma basterebbe estendere questo fallace ragionamento per induzione e troveremmo che 0 è uguale a qualsiasi numero. Pertanto non solo decadrebbero le sue proprietà rispetto alla moltiplicazione e addizione ma a il concetto stesso di calcolo, di quantità cadrebbe meno. Ogni numero sarebbe uguale a qualsiasi altro.
Vi bastano come contraddizioni?
Pertanto l’espressione
1+1+1+1+1+1+1+1+1+1+1+1x0+1 = 1
NON È VERA